효율적으로 약수를 구하는 방법

파이썬으로 약수(divisor)를 구하는 방법을 살펴보겠습니다.

만들다 보니 여러수를 입력해 공약수와 최대 공약수까지 구하도록 확장시켜 보았습니다.

예를 들면 12의 약수는

• 12를 1(n)부터 12(n)까지 나누기 한 후 나머지가 0이면 n은 약수

• 12 / 1 = 나머지 0 이므로 1은 약수

• 12 / 2 = 나머지 0 이므로 2도 약수...(반복)

 따라서 12를 나누어 떨어지는 수는 1, 2, 3, 4, 6, 12 입니다.


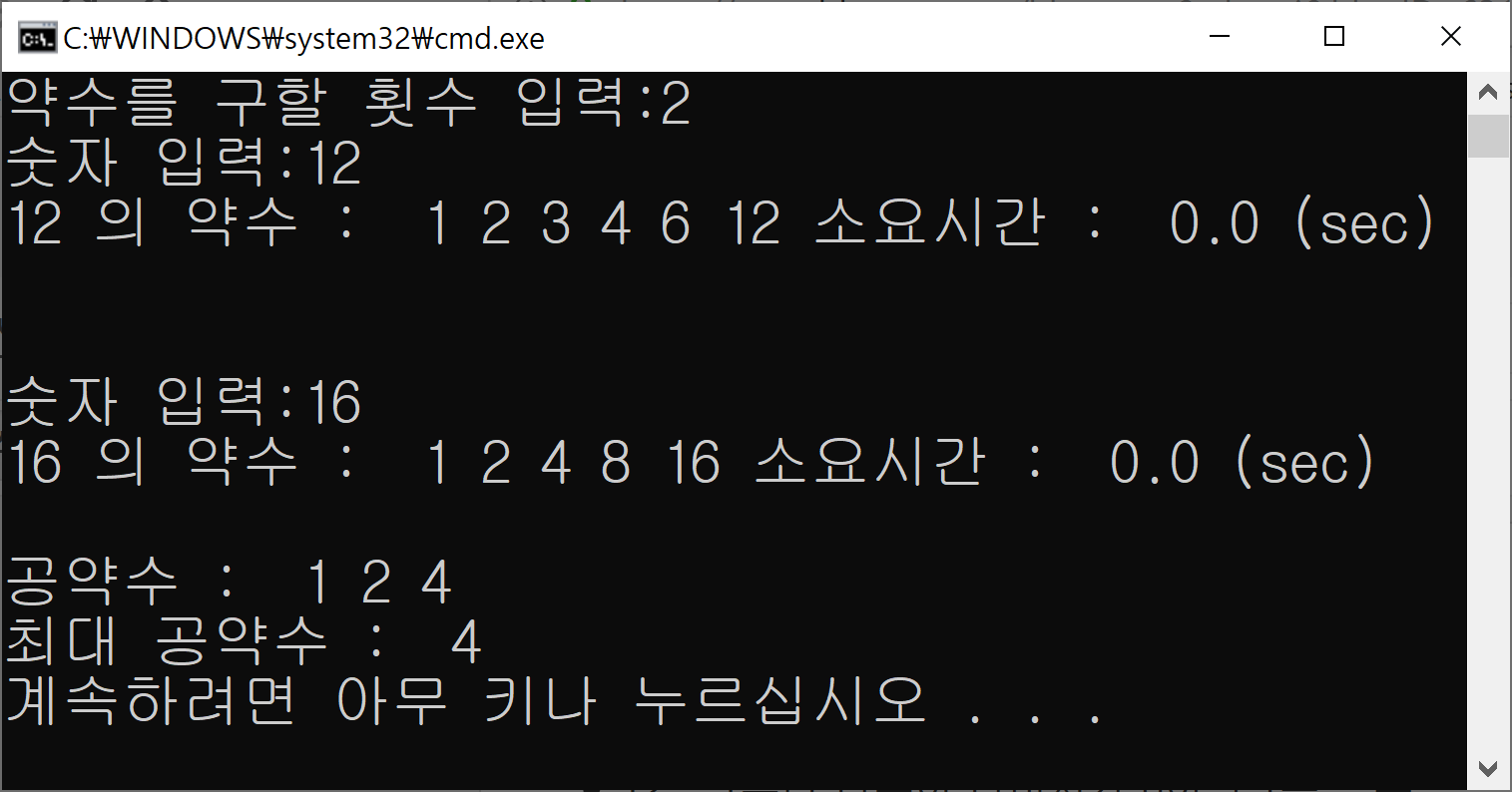
만약 12와 16의 공약수를 구한다면

• 12의 약수 : 1, 2, 3, 4, 6, 12

• 16의 약수 : 1, 2, 4, 8, 16

• 12와 16의 공약수 : 1, 2, 4

• 따라서, 최대공약수는 4

[여러수의 약수, 공약수, 최대공약수 구하기]

조건 

위 방식을 이용해 아래 미션을 수행해 보았습니다.

• 100,000,000의 약수를 구하라. (일억)

방법 1 :

• 단순하게 1부터 약수를 구하고자 하는 수까지 반복

import time

cnt = int(input('약수를 구할 횟수 입력:'))

divs = []

for i in range(cnt):
    n = int(input('숫자 입력:'))

    d = []
    s = time.time()
    for i in range(1, n+1):
        if n%i == 0:
            d.append(i)

    divs.append(set(d))
    print(n,'의 약수 : ', *d, '소요시간 : ', time.time()-s,'(sec)')
    print()
    
if cnt>1:
    comdiv = set.intersection(*divs)
    print('공약수 : ', *comdiv)
    print('최대 공약수 : ', max(comdiv))

약수는 잘 구해지지만 100,000,000 (1억) 의 약수를 구하니 시간이 너무 오래 걸립니다.

제 컴퓨터가 느려서 그런건 아니고 위 코드는 개선할 수 있는 여지가 많이 보입니다.

• 시간 복잡도 O(n) , 소요시간 약 13초 

방법 2 :

• 12(n)의 약수 1, 2, 3, 4, 6, 12 중 자신을 제외한 가장 큰 약수는 n/2 이므로,

• 12의 반인 6까지만 약수 검사를 진행

import time

cnt = int(input('약수를 구할 횟수 입력:'))

divs = []

for i in range(cnt):
    n = int(input('숫자 입력:'))

    d = []
    s = time.time()
    for i in range(1, n//2+1):
        if n%i == 0:
            d.append(i)
    d.append(n)

    divs.append(set(d))
    print(n,'의 약수 : ', *d, '\n소요시간 : ', time.time()-s,'(sec)')
    print()
    
if cnt>1:
    comdiv = set.intersection(*divs)
    print('공약수 : ', *comdiv)
    print('최대 공약수 : ', max(comdiv))

방법 1과 비교해 바뀐 부분은 12번 라인 n//2+1 뿐입니다.

파이썬에서 '/' 나누기 연산자를 두번 '//'쓰면 나머지 소수점을 버린 몫을 얻습니다.

예를 들면 5/2 = 2.5 이지만 5//2 = 2 입니다.

• 시간 복잡도 O(n/2) , 소요시간 약 7초

방법 3 :

•  12(n)의 약수는 1, 2, 3, 4, 6, 12

• 1X12, 2X6, 3X4, 대칭으로 4X3, 6X2, 12X1 

• 따라서 12에 루트를 씌운 수 1, 2, 3, 까지만 반복

• 그리고 현재까지 구해진 약수 1, 2, 3을 이용

• n/1=12, n/2=6, n/3=4 을 통해 약수 구하기 

• 단 제곱수는 두번 약수에 더해지지 않도록 주의

• 예를 들면 9의 약수 1X9, 3X3, 9X1 에서 제곱수(3)

import time

cnt = int(input('약수를 구할 횟수 입력:'))

divs = []

for i in range(cnt):
    n = int(input('숫자 입력:'))

    d = []
    s = time.time()
    for i in range(1, int(n**0.5)+1):
        if n%i == 0:
            d.append(i)
            if i!=n//i:
                d.append(n//i)

    divs.append(set(d))
    print(n,'의 약수 : ', *d, '\n소요시간 : ', time.time()-s,'(sec)')
    print()
    
if cnt>1:
    comdiv = set.intersection(*divs)
    print('공약수 : ', *comdiv)
    print('최대 공약수 : ', max(comdiv))

파이썬에서 '**' 은 제곱을 이므로, n의 0.5 승 즉, 루트를 의미합니다.

import math 구문을 통해 math.sqrt(n) 으로도 사용 가능합니다.

• 시간 복잡도 O(sqrt(n)) , 소요시간 약 0.001초

방법 1, 방법 2에 비해 약 13,000배 빠른 결과를 보입니다.

1억의 약수를 구하는데 sqrt(100,000,000) = 10,000 번의 반복만 수행한 결과입니다.


마지막으로 최대공약수를 구하는 방법은 python의 import math 후 math 모듈의 math.gcd(x, y) 를 통해 쉽게 구할 수 있습니다.

하지만, 위 코드에서 파이썬의 집합(set) 자료형을 통해 약수의 집합을 구성한 후, 각 집합의 교집합(intersection)을 통해 공약수를 찾는 방법을 사용하였습니다.

우리의 목적은 프로그래밍 공부이며, 코드의 구현이 아니기 때문입니다.

사용하기 쉬운 라이브러리나 내장함수만 사용해서는 실력이 늘지 않습니다.


감사합니다.